TL;DR: I saw a random dice game on social media with no satisfying solutions in the comments, so I played around with it using simulation to test my intuition and then worked out the optimal strategy using dynamic programming.
The game
The game has $n$ rounds. You start with $0$ dollars and a 20 sided die (d20) showing the number $1$. Each round, you can take money equal to the number shown, or reroll.
What is the optimal strategy?
In the case where the number of rounds is $100$, the top two most common solutions in the comments were:
- Roll until you get a 20, then keep taking the money
- Roll until you get an 11 or greater, then take the money
They both sort of made sense. In the first case - you are likely to get a 20 in 20 rolls on average, so if you assume that you need to waste 20 rolls making no money, you’ll still have 80 rolls on average left to rake in $ 80 * 20 = \$1600 $. So you’re sort of investing up front to make the max during the later rounds.
The reasoning for the second case is that once you get an 11 or greater - you’re more likely to decrease the value on the die with the next roll than increase it, so you should take the money and run. On average, you’ll get an 11 or greater in 2 rolls, leaving you with 98 rolls to reap your winnings. Sometimes you’ll be lucky and have a 20 for those 98 rolls - but other times you’ll be stuck with 11 - the average is $15.5$. So you’ll end up with $ 98 * 15.5 = \$1519 $ on average with this strategy.
What was bothering me though was no one in the comments mentioned how the best strategy should depend on the “state” of the game (the number of rounds left and the current value of the die).
This is really easy to see if you play with different values of $n$. For example, if $n = 1$, the best strategy is to take your measly dollar and run, rerolling won’t help you.
If $n = 2$, the best strategy is to roll once, here’s what could possibly happen:
- If you roll a 1 - you’ll get a dollar, bummer because you could have had \$2 if you stuck with it last round, chances of this happening are 1/20
- If you roll a 2 - you’ll get \$2, chances of this happening are 1/20, and kind of the same boat as if you had stuck with your 1 last round
- Otherwise, you’re making money - if you roll a 3-20, you’ll get between \$3 and \$20, each of those have a 18/20 chance of coming up
So you roll once with n = 2, you’ll end up with \$10.50 on average (average roll of a d20 is 10.5), and only 1/20 times will you be angry at yourself for not sticking with your dollar on the first round.
That’s one end of the spectrum as we run out of rounds. So it seems like our strategy should be less picky as we run out of rounds.
On the other end, when we have plenty of rounds left, we can afford to be more patient and wait for a better roll. For example, if $n = 1000$, it’s not a great strategy to take an 11 on the first roll, because you’ve got plenty of rounds to go and you’ll probably end up with a 20 or another high roll with plenty of time left.
So that’s the intuition - but working out the optimal strategy on paper is proving to be a bit tricky. To check my intuition, I wrote a quick simulation in python
Simulations
You can see and run the code in this notebook, the main idea is that we can implement a bunch of strategies and see which ones are best. Here’s a couple of examples:
# Some example strategies
def do_nothing_strategy(current: int, remaining: int, _:int):
""" Just take the 1, man """
return current, current
def random_strategy(current: int, remaining: int, _: int):
""" Chaos - decide to roll or take randomly """
if random.randint(0, 1) == 1:
return roll(), 0
return current, current
def roll_once_strategy(current: int, remaining: int, total_rounds: int):
""" Reroll the first round and take what we get """
if remaining == total_rounds:
return roll(), 0
return current, current
def reroll_non_20_strategy(current: int, remaining: int, _: int):
""" Reroll non-20s """
if current < 20:
return roll(), 0
return current, current
def take_greater_than_10(current: int, remaining: int, total_rounds: int):
""" Take anything greater than 10 - 10.5 is the average roll """
if current > 10:
return current, current
return roll(), 0
And then we can play the game with each strategy, average the profits for each over a bunch of runs, and see how they compare - the full code is the notebook, but here’s the snippet to play the game and the average it a bunch of times:
def play_game(n_rounds: int, strategy: StrategyFunction):
""" Play a game of n_rounds using the supplied strategy """
profit = 0
current = 1
for round in range(n_rounds):
current, take = strategy(current, n_rounds - round, n_rounds)
profit += take
return profit
def ensemble(
runs: int,
strategy: StrategyFunction,
rounds_per_game: int
) -> float:
""" Average a bunch of repeats together """
profit = 0
for run in range(runs):
profit += play_game(rounds_per_game, strategy)
return profit / runs
Finally - with the simple tooling in place, we can play the game a bunch of times and see how the strategies compare. Here’s a plot of the average profit for each strategy as we vary the number of rounds:
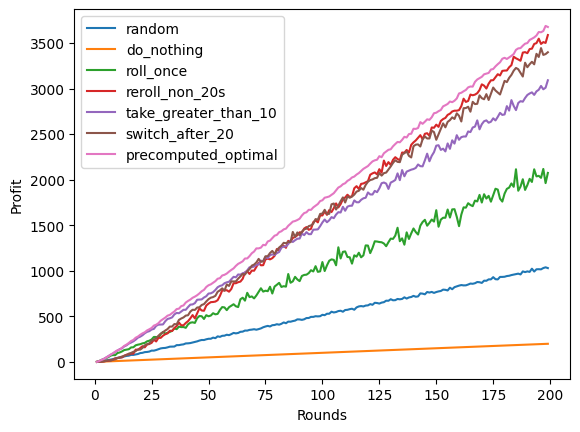
There are some interesting things to note here. At the start, the “take greater than 10” strategy is better than the “roll until 20” strategy - but as we run longer, the “roll until 20” strategy takes over. They both have a short “explore” phase where they’re rerolling until they get to their respective thresholds, but they settle afterward - with the “roll until 20” strategy winning.
Clearly the best strategy is going to be some kind of function of the current round and the current value on the die.
Spoiler alert: The optimal strategy profit is also shown on the plot above.
But how can we work it out? I’m still not sure how to get to to a closed form solution, but we can work it out and build a decision tree by working backwards from the end of the game and using dynamic programming.
Dynamic programming - build the decision table
To build the decision table, we’ll work backwards from the end of the game. We can save the best choice for any given state (current value on the die, number of rounds left) for later - then when we run the actual game, we look up the best choice using the current game state and follow that path.
Here’s the idea for the top down approach:
- Start with the last round - what’s the best choice?
- In the last round, as we saw before - you should take anything - there’s no reason to reroll.
- Work our way back to the first round, at each round we could either keep the current value, or reroll.
- If we keep the current value, we’ll get the current value on the die, plus whatever this die roll will be worth in future rounds.
- If we reroll, we’ll get the average of all the possible rolls (1-20) in the next round.
So we’ll make a table $dp[r][value]$ that has the expected value for each possible state. The base case is $r = n$, where we just take the current value.
So $dp[n][value] = value$ for all $value$ (1, 2, 3, …, 20).
Now we can work our way back to the first round, using the following recursive relation:
$$ keep = value + dp[r+1][value] \quad \forall value \in (1, 2, 3, …, 20) $$ $$ reroll = \frac{1}{20} \sum_{roll=1}^{20} dp[r+1][roll] $$ $$ dp[r][value] = max(keep, reroll) $$
When we get to the start, we’ll have a table with the expected value of each possible game state.
Since we’re interested in the best decision for each state so that we can use this in simulation, we’ll also keep track of the decision that was made for each state (eg was it keep or reroll) along the way.
Here’s the code to build the tables:
@cache
def get_optimal_solution(n: int) -> list[list[int]]:
""" Using dynamic programming to get the optimal solution
Return a decision table that will tell you to take or
reroll at each state. The state is the current round and the
number on the D20, so the table is:
decision_table[r][v-1] = round r, with value v showing
=> (1) if you should accept or
(0) if you should reroll
"""
decision_table = [[0 for _ in range(20)] for _ in range(n+1)]
dp = [[0 for _ in range(20)] for _ in range(n+1)]
# base cases - we always have to take on the final roll - no reason
# to ever reroll it
for v in range(1, 21):
decision_table[n][v-1] = 1
dp[n][v-1] = v
# go backwards
for r in range(n-1, -1, -1):
# dp[r][v-1] = max(accept, reroll)
# reroll - same expected value for any current face value so we
# can compute it here
reroll_ev = sum(dp[r+1][i-1] for i in range(1, 21)) / 20.0
# accept will depend on each current value
for v in range(1, 21):
accept_ev = dp[r+1][v-1] + v
if accept_ev > reroll_ev:
# keeping it on to next round
decision_table[r][v-1] = 1
dp[r][v-1] = accept_ev
else:
# reroll is better outcome
decision_table[r][v-1] = 0
dp[r][v-1] = reroll_ev
return decision_table
We can inspect the table a bit to see what it tells us - for example - when you get to 3 rounds left, you should reroll anything less than 7, with 10 rounds left, you should reroll anything less than 13, once you get to 50 rounds left you should reroll anything less than 17, and so on - here’s a plot of the threshold as a function of the number of rounds:
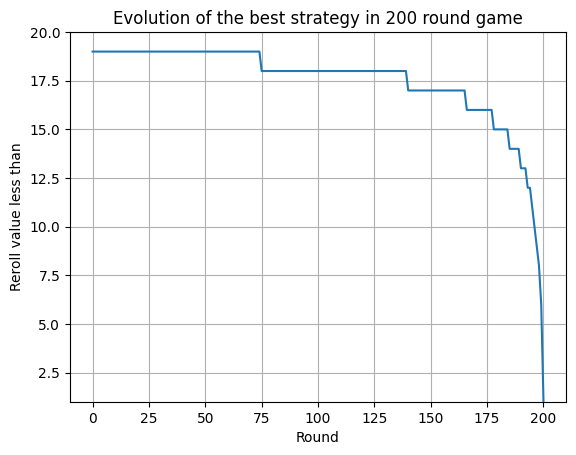
So our threshold is moving as we run out of rounds as we thought. Taking another look at the first plot:

The optimal strategy we pre-computed beats all the other simple strategies that we have come up with.
I’m still wondering if there’s a closed form solution for the optimal strategy, but my math is a little rusty so I haven’t been able to work it out yet.
If you see a different solution please let me know!